Introducción
Que las matemáticas están presentes en nuestra vida cotidiana no es algo nuevo. Y que una de las aficiones más destacada del mundo, el deporte, está lleno de matemáticas, tampoco sería una novedad. Nosotros vamos a estudiar la actividad física y las matemáticas a través del arte, ¿o era la EF y el arte a través de las matemáticas, o el arte y las matemáticas a través de la EF? Da igual como fuese, los tres campos vamos a estudiarlos interrelacionándolos y realizando un pequeño recorrido a través de la historia y a través de pequeños retos educativos. ¿Te atreves?
GRECIA, EL OLIMPISMO Y EL ARTE
Hay mucha de arte, matemáticas y obviamente, de deporte en los creadores de uno de los eventos deportivos más importantes de todos los tiempos, los griegos. Sus valores y espíritu religioso hacia que para ellos el deporte fuese algo casi sagrado.
Investigamos sobre los orígenes del Olímpismo y descubrimos como sus ceramistas y escultores reproducían en sus obras cada una de las pruebas que constituían el movimiento olímpico de la época. Si queremos hablar de pintura griega es necesario hacer referencia a la cerámica, ya que precisamente en la decoración de ánforas, platos y vasijas, fue donde pudo desarrollarse el arte. Los temas de palestra, de entrenamiento de atletas y de competiciones son las temáticas más abundantes.
Respecto a la escultura griega, el cuerpo humano desnudo era el tema central. El Discóbolo de Mirón es una de las más excelsas obras maestras y se realizó en el 455 a.c. y representa el cuerpo de un atleta en el instante antes de lanzar el disco.
Muchas esculturas y obras, todavía permanecen en muchos museos y, gracias a estos, podemos conocer como era la actividad física y el deporte en aquella época. También en dicha época se construyeron edificios cuyo uso era exclusivamente deportivo. Los estadios eran de planta rectangular, con gradas a los lados. Uno de los lados tenía forma semicircular y el otro en forma de recta. La longitud de la pista era de 212,54 m (697,3 pies) de largo y 28,5 m (94 pies) de ancho, y está rodeada por bancales de hierba. Minireto: ¿A cuántos cms puede equivaler un pie?
Los primeros Juegos Olímpicos se desarrollaron en el 776 a.c.
Te propongo otro minireto matemático:
Matemáticamente, ¿cómo representarías esa fecha?
a) +776 b) 0 c) -776
Muchas esculturas y obras, todavía permanecen en muchos museos y, gracias a estos, podemos conocer como era la actividad física y el deporte en aquella época. También en dicha época se construyeron edificios cuyo uso era exclusivamente deportivo. Los estadios eran de planta rectangular, con gradas a los lados. Uno de los lados tenía forma semicircular y el otro en forma de recta. La longitud de la pista era de 212,54 m (697,3 pies) de largo y 28,5 m (94 pies) de ancho, y está rodeada por bancales de hierba. Minireto: ¿A cuántos cms puede equivaler un pie?
Los primeros Juegos Olímpicos se desarrollaron en el 776 a.c.
Te propongo otro minireto matemático:
Matemáticamente, ¿cómo representarías esa fecha?
a) +776 b) 0 c) -776
Te propongo el segundo de los miniretos matemáticos. ¿Serías capaz de conseguir realizar este puzzle en menos de 300 segundos? ¿Qué cuantos minutos son 300 segundos? Ya sabes como calcularlo, a través de una operación fácil. Pista: deberás saber cúantos segundos hay en un minuto.
RETO: PUZZLE SOBRE EL ARTE GRIEGO (haz click en el enlace)
RETO: PUZZLE SOBRE EL ARTE GRIEGO (haz click en el enlace)
A continuación te dejo un fragmento de un cómic sobre las olimpiadas por si deseas colorearlo:
MATEMÁTICAS, ARTE E IDEAL DE CUERPO HUMANO
EN LEONARDO DA VINCI
Una de las figuras más importantes en el campo del arte, las matemáticas e incluso del estudio del cuerpo humano fué, sin lugar a dudas, Leonardo da Vinci. Un genio, inventor y artista que vivió en los siglos XV y XVI. A él le debemos la noción de la perspectiva, que sigue siendo de utilidad a todos los artistas. Quizás, de las obras más famosas que posee, sin lugar a dudas, es el hombre de Vitruvio. Un dibujo sobre el cuerpo humano basado en múltiples datos matemáticos que lo podrás en cualquier lugar del mundo. Al
retomar por su cuenta este dibujo, Leonardo da Vinci estableció diferentes
medidas sobre un cuerpo humano, definido como “perfecto”. Entre ellas,
descubrimos que, al extender las piernas, el espacio que se crea en el suelo y
la figura formada por nuestras piernas forman un triángulo equilátero; o que la
longitud total de nuestros dos brazos estirados es igual a nuestra altura.
Este dibujo le permitió medir con precisión
cada parte del cuerpo en proporción al conjunto. Así mismo, el simple hecho de
inscribir a este hombre en un círculo y un cuadrado muestra la importancia de
la geometría y de las matemáticas para este famoso pintor y dibujante. Este mismo dibujo, se utiliza en numerosas obras de EF o de deportes.
RETO: ¿SERÍAS CAPAZ DE REALIZAR ESTE ROMPECABEZAS?
LOS JUEGOS POPULARES EN LAS OBRAS DE GOYA
Goya, fué un pintor español, que nació en 1746 y murió en Francia en el 1828. Minireto: ¿En qué siglos vivió Francisco de Goya teniendo en cuenta los años de su nacimiento y su muerte?
Goya, fué un pintor español, que nació en 1746 y murió en Francia en el 1828. Minireto: ¿En qué siglos vivió Francisco de Goya teniendo en cuenta los años de su nacimiento y su muerte?
Fue el artista europeo más importante de la época ya que se consideró que con sus últimas obras fue el precursor del impresionismo. Entre otras obras, pintó numerosos cuadros y tapices sobre juegos populares de la época. Ahí se aprecia como la nobleza madrileña se divertía en su tiempo de ocio mientras el resto de la población trabajaba.
Realiza un visionado de los tapices y cuadros de Francisco Goya en el siguiente enlace. Una vez finalizado, ya puedes realizar el próximo reto.
Realiza un visionado de los tapices y cuadros de Francisco Goya en el siguiente enlace. Una vez finalizado, ya puedes realizar el próximo reto.
RETO: MEMO CON CUADROS DE GOYA
Te reto a que consigas realizar el Memo sobre los cuadros de Goya en menos de 10 minutos. ¿Te atreves? Coge un reloj y apunta el tiempo que hayas tardado en lograrlo.
Brueguel El viejo: "LOS JUEGOS DE LOS INFANTES".
Observa con detenimiento estos vídeos que te dejo en estos enlaces:
En el siglo XVI, Brueguel El viejo, pinta el cuadro "Paisajes del Juego", retratando la realidad cotidiana de su país, Holanda. En este cuadro nos muestra a X números de niños jugando en la plaza del pueblo a X números de juegos de aquella época. Digo X (incógnita matemática) porque ese es parte del gran reto.
EL GRAN RETO: ACERTAR EL NÚMERO DE JUEGOS Y DE NIÑOS JUGANDO EN ESTE CUADRO.
¿Serías capaz de acercarte al verdadero número de juegos que se puede apreciar en la imagen? ¿Cuántos niños/as aparecen el cuadro? Te dejo un margen de error del 10%
Como mínimo deberás escribir al menos el nombre de estos 15 juegos.
Si te atreves a buscar todos o el mayor número de juegos, para llevar a cabo el recuento, te puedo dar pequeñas pistas o herramientas, y es que puedes utilizar las matemáticas para poder realizarlo. Por ejemplo, puedes dividir el cuadro en pequeñas parcelas o cuadrantes , dibujando dos líneas paralelas horizontales y otras dos verticales, de este modo:
De esta forma, podrás ir anotando los juegos por cada parcela.
La distancia con la que se pinta el cuadro y el detalle de cada figura, hace necesario que te acerques y a su vez que te alejes para poder apreciar los juegos y a los niños.
Ahora te reto a que consigas ponerme en qué cuadrante se encuentra cada escena teniendo en cuenta los cuadrantes del dibujo anterior.
Ejemplo: Este dibujo lo podemos encontrar en el cuadrante B1
¿En qué cuadrante podremos encontrar estos?
Por último, te dejo el cuadro por si deseas imprimirlo y colorearlo. Así podrá tener tu propia obra de arte en casa.
Te dejo otro enlace para que conozcas un poco más de esta grandiosa obra:
Y POR ÚLTIMO...CURIOSIDADES
El partido de tenis más largo de la historia
Si lo que te gustan son los números en cualquier sitio, te contaremos los que aparecen en uno de los partidos más largos de la historia del tenis. 𝓔l partido interminable es un encuentro de tenis muy famoso porque persistirá durante años en la retina de los aficionados a este deporte. 70-68. Así acabó el quinto set del partido más largo de la historia del tenis. Nada más y nada menos que 11 horas y 5 minutos.𝓔l partido nos deja más récords: 183 juegos, cuando el récord estaba en 112; 215 aces entre los dos, de los que 112 fueron para Isner y 103 para Mahut, superando ampliamente ambos el récord de Karlovic de 78, 490 golpes ganadores...
Geometría de un balón
¿Sabías que en los balones de fútbol hay mucha geometría incorporada? ¿Creías que el balón de fútbol es esférico como te lo contaba el maestro en sus ejemplos? Pues no es del todo cierto.
Se trata del icosaedro truncado; un poliedro así llamado por ser el que se obtiene cuando a los icosaedros le cortamos las esquinas a distancias iguales de cada vértice.
𝓔stá formado por 20 hexágonos regulares y 12 pentágonos regulares; y tiene 90 aristas. Este poliedro ocupa un volumen del 86,74% de la esfera circunscrita; porcentaje que aumenta hasta el 95% al ser inflado del balón de fútbol. Aún así, el balón no sería totalmente esférico. De hecho,
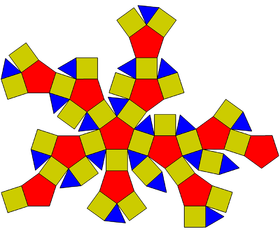
Imagen del balón por número de figuras geométricas.
existe otro poliedro que permitiría conseguir balones más esféricos. Se trata del rombicosidodecaedro (¡toma ya!), cuyas caras son 20 triángulos equiláteros (lados iguales), 30 cuadrados y 12 pentágonos regulares; tiene 120 aristas y antes de ser inflado ya ocupa más el 94,5% de la esfera. Pero debes saber que los fabricantes de balones no ha adoptado esta solución porque aumenta bastante la complejidad de la fabricación (120 costuras que coser, frente a las 90 del icosaedro truncado). ¿Qué pasaría si se fabricaran balones más esféricos? Pues seguramente, que muchos goles o fallos que has visto por la TV, no se hubiesen producido nunca, porque hubiesen botado o rodado de diferente manera y los vórticex (las parábolas que toman) hubiesen sido diferentes.
ESPERO TE HAYA GUSTADO ESTE PROYECTO DE RETOS
No hay comentarios:
Publicar un comentario